1. Az alapképlet fizikai elvének ellenőrzése
A tömegmegmaradás törvénye
Minden képlet az m=ρ×V (tömeg = sűrűség × térfogat) fizikai természetén alapul.
Sűrűségérték
A tiszta alumínium elméleti sűrűsége: 2698 kg/m³ (20 ℃)
A 2700 kg/m³ hozzávetőleges érték ipari számításokhoz elfogadható (hiba < 0,1%).
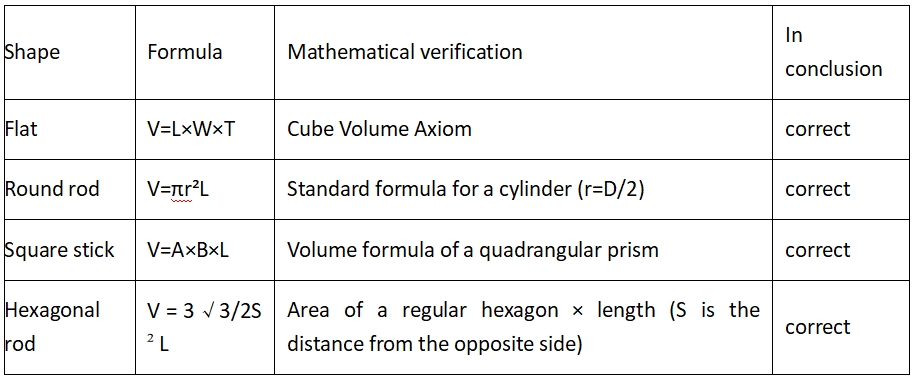
2. A geometriai képletek szigorúságának ellenőrzése
2.1. Standard geometriai térfogatképlet
Négyzet alakú cső formulájára vonatkozó korlátozások:
Ez akkor igaz, ha a cső falvastagsága egyenletes, és a belső szög derékszög (a tényleges négyzet alakú cső átmenete lekerekített, és az elméleti hiba körülbelül 1-3%).
3. Egységrendszer konzisztenciájának ellenőrzése
Egységek közötti számítás kockázati pont vizsgálata
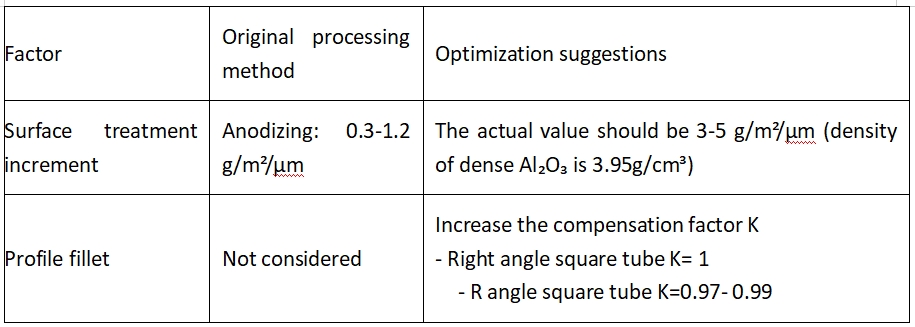
4. Mérnöki Alkalmassági Módosítás
4.1. Nem ideális tényezők kompenzációja
4.2. A tolerancia hatásának számszerűsítése
Vastagságtűrés ±10% → Súlyeltérés ±(8% ~ 12%) (a vékony falú alkatrészek érzékenyebbek)
Megoldás: W tényleges = W elméleti × (1 + Δt / t) (Δt : vastagságeltérés)
5. Határfeltétel-teszt
Szélsőséges esetek ellenőrzése:
Sűrűségi anomália forgatókönyv
7xxx ötvözet (7075): Mért sűrűség 2,810 g/cm³ → Ha véletlenül 2,7 g/cm³-t használnak, a hiba +4,1%.
Képlettáblázat
A 4t(A + B)- 4t² egy szabványos mérnöki számítás, amelyet úgy számítanak ki, hogy a keresztmetszet kerületét megszorozzák a falvastagsággal, majd levonják a négy sarokpontot.
Számítási példa:
1.6061 alumínium lemez(1000 × 500 × 10 mm, hossz 2 m): Sz = 1000 × 500 × 2 × 0,0027 = 27 kg
2,7075 kerek cső(külső átmérő 50 mm, falvastagság 3 mm, hosszúság 1,5 m): W = [(50-3)×3×3,1416×1,5]×0,00283 ≈ 5,65 kg
3. Négyzet alakú cső(40 × 40 × 2 mm, hossz 3 m): Tömeg = [2 × 2 × (40 + 40 - 4) × 3] × 0,0027 × 0,98 ≈ 2,42 kg
Ajánlott munkafolyamat
1. Sűrűség kiválasztása → 2. Tényleges méret mérése → 3. Kompenzációs tényező kiválasztása → 4. Képlettel való számítás
Közzététel ideje: 2025. június 17.